Odd or Even é como dizem nossos amigos ingleses quando querem decidir algo de forma rápida e justa.
Existem várias fórmulas de escolha, mas o milenar “par ou ímpar” é um dos mais utilizados até hoje. Aluísio A. (1946) descreve esta fórmula de escolha da seguinte maneira: Os dois jogadores ou os dois diretores do jogo ficam à frente, um diz: - Par! , o outro diz; Ímpar! Ou vice-versa, mantendo a mão direita fechada atrás. Trazem as mãos para frente com a palma para baixo, simultaneamente, apresentando de zero a cinco dedos. Somam-se os números. Se a soma é um número par, ganhou o que disse "par" e se a soma é um número ímpar, ganhou o que disse “ímpar”.
Estimasse que hoje, somente no Brasil, somos mais de 30 milhoes de jogadores frequentes. e mais de 80 mi de jogadores esporádicos.
Dizem que primeiro o brasileiro aprende a cantar "parabens para voce" e depois a jogar par ou ímpar.
O numero de praticantes só cresce no Brasil e graças a isso estamos coletando assinaturas para incluir o Par ou Ímpar nos jogos olímpicos do Rio em 2016
segunda-feira, 7 de fevereiro de 2011
Zero é par ou ímpar ??
Agora solucionaremos uma das grandes dúvidas de vários amigos jogadores, mas como somos orgulhosos não perguntamos para ninguem:
ZERO É PAR OU ÍMPAR ??
Por convenção o número zero é par. Quer dizer, é conveniente adotar o número zero como par. Por que é conveniente colocar o zero como par? Algumas respostas:
1) Os números pares e ímpares aparecerão alternados. Isto é,
0 (par) , 1(ímpar), 2(par), 3(ímpar), etc
Note a alternância: par, ímpar, par, ímpar, ...
2) o subconjunto dos números pares terão a seguinte propriedade:
A soma de dois números pares é também um número par. Exemplos 2 + 4 =6; 0 + 8=8 etc.
3) os números pares seriam aqueles que dividindo por 2 temos resto igual a zero. Exemplos 4 : 2 = 2 com resto da divisão igual a zero. 5 : 2=2 com resto 1.
As respostas 1),2) e 3) justificam o porquê de convencionar o zero como par.
Porém o numero zero não seria par por definição. Para entender isto é necessário entender a definição de par. Por definição, um número é dito par se em sua representação por tracinhos, cada tracinho tem o seu par. Imagine em um baile cada um tem o seu par. Daí vem o nome par. Agora veja os exemplos numéricos:
3 = | | |
O que está acima representação do número 3 por tracinhos.
Note, que neste caso, temos um par (o primeiro como o segundo tracinho) mas fica sobrando um tracinho( o 3º tracinho) sem seu par. Analogamente
5 = | | | | |
Note que o 5º tracinho ficará sem par.
Vemos que o 5 pela definição acima (definição via tracinhos) é não par (dize-se ímpar). Mas
4 = | | | |
o número 4 é par. (Aqui cada tracinho tem o seu par).
Assim o número 1 = | é obviamente não par (ímpar). (Aqui há um tracinho que não tem o seu par). Agora finalmente podemos entender o que acontece como o número zero. Veja abaixo a representação do número zero via tracinhos:
0 =
Note que não há tracinho algum. Por isto, não se pode dizer nada a cerca de pares de tracinhos. Isto é, que tracinho fica com que tracinho, pois não há tracinhos! Assim o número zero segundo a definição acima não é par. Também não é impar, pois não sobrou nenhum tracinho sem par.
Conclusão: Zero é um número par por convenção apenas.
Outro situação parecida é o fatorial. Por exemplo:
3! é definido como 3x2x1; 6! é definido como 6x5x4x3x2x1. Desta forma 1! é igual a 1 por definição, mas segundo a definição acima não se pode dizer nada sobre 0!. Porém, devido a fórmulas de combinatória bem conhecidas, por exemplo
(n tomados p a p)= n!/[(n - p)!p!]
e
(a + b)^n = soma_{p=0 até n} (n tomados p a p) a^(n - p) b^p
é que se convenciona adotar 0! como sendo igual a 1.
Moral da estória: Quando estabelecemos uma definição, as coisas ficam mais fáceis de serem entendidas. E no par o ímpar o 0 (zero) é par !!
Se não esta satisfeito leia o estudo abaixo !!
Cosine function: f(x) = cos(x)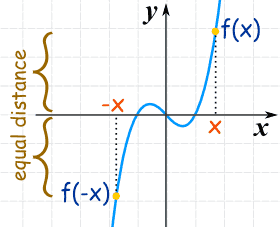
Sine function: f(x) = sin(x)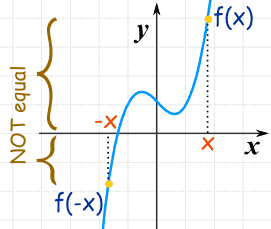
ZERO É PAR OU ÍMPAR ??
Por convenção o número zero é par. Quer dizer, é conveniente adotar o número zero como par. Por que é conveniente colocar o zero como par? Algumas respostas:
1) Os números pares e ímpares aparecerão alternados. Isto é,
0 (par) , 1(ímpar), 2(par), 3(ímpar), etc
Note a alternância: par, ímpar, par, ímpar, ...
2) o subconjunto dos números pares terão a seguinte propriedade:
A soma de dois números pares é também um número par. Exemplos 2 + 4 =6; 0 + 8=8 etc.
3) os números pares seriam aqueles que dividindo por 2 temos resto igual a zero. Exemplos 4 : 2 = 2 com resto da divisão igual a zero. 5 : 2=2 com resto 1.
As respostas 1),2) e 3) justificam o porquê de convencionar o zero como par.
Porém o numero zero não seria par por definição. Para entender isto é necessário entender a definição de par. Por definição, um número é dito par se em sua representação por tracinhos, cada tracinho tem o seu par. Imagine em um baile cada um tem o seu par. Daí vem o nome par. Agora veja os exemplos numéricos:
3 = | | |
O que está acima representação do número 3 por tracinhos.
Note, que neste caso, temos um par (o primeiro como o segundo tracinho) mas fica sobrando um tracinho( o 3º tracinho) sem seu par. Analogamente
5 = | | | | |
Note que o 5º tracinho ficará sem par.
Vemos que o 5 pela definição acima (definição via tracinhos) é não par (dize-se ímpar). Mas
4 = | | | |
o número 4 é par. (Aqui cada tracinho tem o seu par).
Assim o número 1 = | é obviamente não par (ímpar). (Aqui há um tracinho que não tem o seu par). Agora finalmente podemos entender o que acontece como o número zero. Veja abaixo a representação do número zero via tracinhos:
0 =
Note que não há tracinho algum. Por isto, não se pode dizer nada a cerca de pares de tracinhos. Isto é, que tracinho fica com que tracinho, pois não há tracinhos! Assim o número zero segundo a definição acima não é par. Também não é impar, pois não sobrou nenhum tracinho sem par.
Conclusão: Zero é um número par por convenção apenas.
Outro situação parecida é o fatorial. Por exemplo:
3! é definido como 3x2x1; 6! é definido como 6x5x4x3x2x1. Desta forma 1! é igual a 1 por definição, mas segundo a definição acima não se pode dizer nada sobre 0!. Porém, devido a fórmulas de combinatória bem conhecidas, por exemplo
(n tomados p a p)= n!/[(n - p)!p!]
e
(a + b)^n = soma_{p=0 até n} (n tomados p a p) a^(n - p) b^p
é que se convenciona adotar 0! como sendo igual a 1.
Moral da estória: Quando estabelecemos uma definição, as coisas ficam mais fáceis de serem entendidas. E no par o ímpar o 0 (zero) é par !!
Se não esta satisfeito leia o estudo abaixo !!
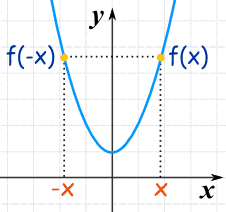
Even Functions
A function is "even" when:
f(x) = f(-x) for all x
In other words there is symmetry about the y-axis (like a reflection):

This is the curve f(x) = x2+1
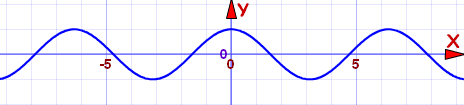
It is called "even" because even exponents like x2, x4, x6, etc behave like that, but there are other functions that do that, too, such as cos(x):

Cosine function: f(x) = cos(x)
Odd Functions
A function is "odd" when:
-f(x) = f(-x) for all x
Note the minus in front of f: -f(x).
And we get origin symmetry:

This is the curve f(x) = x3-x
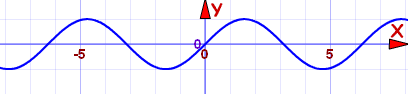
It is called "odd" because odd exponents like x, x3, x5, etc behave like that, but there are other functions that do that, too, such as sin(x):

Sine function: f(x) = sin(x)
Neither Odd nor Even
Don't be misled by the names "odd" and "even" ... they are just names and a function does not have to beeven or odd.
In fact most functions are neither odd nor even. For example, just adding 2 to the curve above gets this:

This is the curve f(x) = x3-x+1
It is not an odd function, and it is not an even function either.
Even or Odd?
Example: is f(x) = x/(x2-1) Even or Odd or neither?
Let's see what happens when we substitute -x:
| Put in "-x": | f(-x) | = (-x)/((-x)2-1) | |
| Simplify: | = -x/(x2-1) | ||
| = -f(x) |
So f(-x) = -f(x) and hence it is an Odd Function
Regra Básica
Muitas pessoas em suas disputas, serias ou não, gostam de decidir através do bom e velho jogo de Par ou Ímpar. Nesse jogo, um dos participantes escolhe Par e o outro Ímpar. Após a escolha, os dois jogadores mostram, simultaneamente, uma certa quantidade de dedos de uma das mãos. Se a soma dos dedos das mãos dos ambos jogadores for par, vence o jogador que escolheu previamente Par, caso contrário vence o que escolheu Ímpar.
Em algumas culturas o jogo de par ou ímpar aceita o uso de duas mãos, mas o modo mais utilizado é com apenas uma mão e o uso de apenas 1 (um), 2 (dois) ou 0 (zero) dedos
Em algumas culturas o jogo de par ou ímpar aceita o uso de duas mãos, mas o modo mais utilizado é com apenas uma mão e o uso de apenas 1 (um), 2 (dois) ou 0 (zero) dedos
Seja Bem Vindo
Este é o nosso primeiro post.
Aqui discutiremos regras e diferentes modos e práticas deste jogo tão básico, divertido e funcional.
Seja Bem Vindo a Confederação Brasileira de Par ou Impar
Aqui discutiremos regras e diferentes modos e práticas deste jogo tão básico, divertido e funcional.
Seja Bem Vindo a Confederação Brasileira de Par ou Impar
Assinar:
Postagens (Atom)
